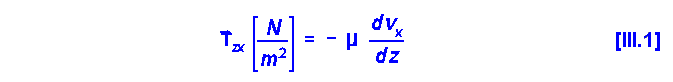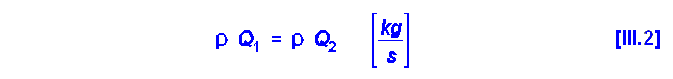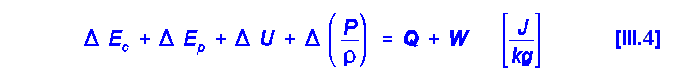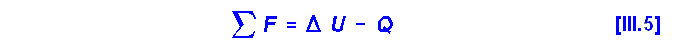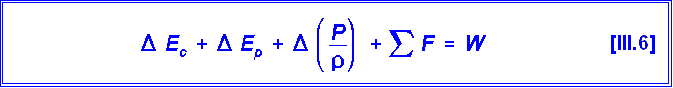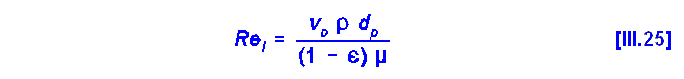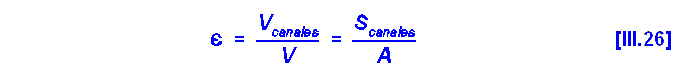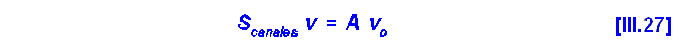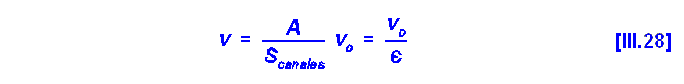TEMA III:

INTRODUCCIÓN AL FLUJO DE FLUIDOS

Importancia de la circulación de los fluidos: Disciplina propia.

Estudio del movimiento de líquidos y gases:

• Interés práctico (bombeo de agua de pozos, sistemas de riego).
• Interés industrial (gaseoductos, oleoductos, túneles de viento).

Fundamentos basados en ecuaciones que describen:

• Comportamiento del movimiento (velocidad, presión).
• Pérdidas de energía por rozamiento.

Las ecuaciones relacionan estas variables y permiten:

• Calcular la potencia necesaria para el flujo.
• Medir el caudal.

Interés en Ingeniería Química, con tratamiento teórico diferente:

• Flujo interno: Circulación por conducciones.
• Flujo externo: Circulación alrededor de sólidos sumergidos.

Ecuación cinética de transporte molecular de cantidad de movimiento (ley de Newton):

Ecuación experimental en la que m (viscosidad) es una propiedad física que sólo depende de la temperatura.

• Fluidos que obedecen la ley de Newton: fluidos newtonianos.
• Fluidos que no se comportan según la ley de Newton: fluidos no newtonianos.

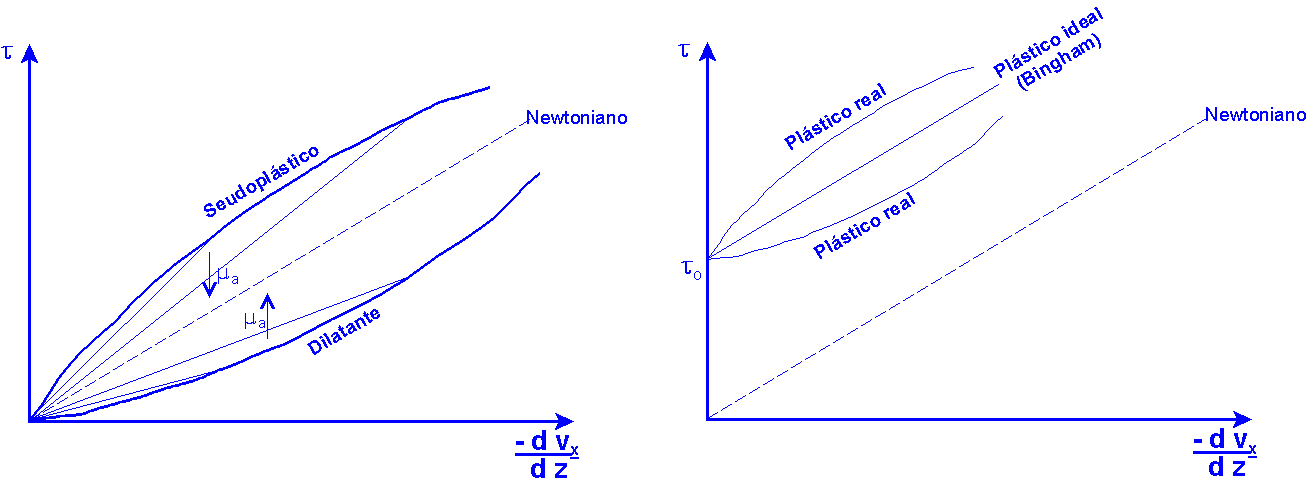
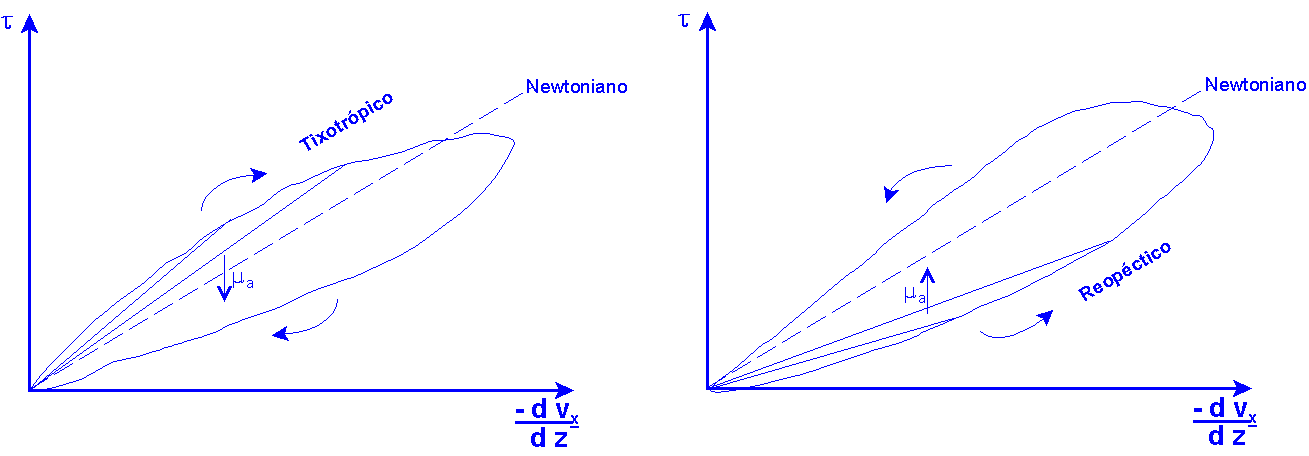
Reología: Disciplina que se ocupa de los cuerpos deformables; se aplica a estudios esfuerzo - deformación para determinar la "viscosidad aparente" de los fluidos no newtonianos.

Se estudiarán dos grupos de fluidos no newtonianos:

• Fluidos independientes del tiempo.
• Fluidos dependientes del tiempo.

• Seudoplásticos: Su viscosidad aparente disminuye al aumentar el gradiente de velocidad (pulpa de papel, zumos de frutas, mayonesa, compotas, mermelada, sopas preparadas).
• Dilatantes: Su viscosidad aparente aumenta al aumentar el gradiente de velocidad (suspensiones de almidón, goma arábiga).

• Plásticos: Presentan un valor de tensión, t_o, denominado "esfuerzo de deformación umbral", que debe ser superado para que el compuesto comience a fluir:
• Plástico de Bingham (ideal): Por encima del esfuerzo umbral, se comporta como si fuese newtoniano (pasta de dientes, suspensiones de arcilla en agua).
• Plástico real: Por encima del esfuerzo umbral, se comporta como no newtoniano, con aumento o disminución de la viscosidad aparente con la deformación (margarinas, mantequillas, puré de manzana).

• Tixotrópicos: La velocidad de destrucción prevalece sobre la de regeneración con el aumento del gradiente y del tiempo, por lo que la viscosidad aparente disminuye con ellos; una vez dejado en reposo el fluido, su estructura se reconstruye gradualmente (salsa de tomate, pintura: al agitar aumenta su fluidez, en reposo vuelven a recuperar su consistencia).
• Reopécticos: La velocidad de regeneración prevalece sobre la de destrucción con el aumento del gradiente y del tiempo, por lo que la viscosidad aparente aumenta con ellos; una vez dejado en reposo el fluido, su estructura se desorganiza gradualmente (suspensiones de arcilla, coloides: al agitar aumenta su consistencia, en reposo vuelven a recuperar su fluidez).

La circulación de un fluido por el interior de una conducción se produce con pérdidas por rozamiento debidas a la viscosidad, por lo que hay que reponer la energía para mantener el flujo.

El diseño implica el cálculo de:

• Pérdidas por rozamiento.
• Potencia para la impulsión.

Utilización de balances macroscópico simplificados:

• Fluido incompresible (densidad constante).
• Circulación en estado estacionario (invariante con el tiempo).

o también (ecuación de continuidad):

Balance macroscópico de energía total aplicado al elemento:

Los factores más significativos son las formas mecánicas; las no mecánicas se engloban en un término positivo llamado pérdidas por rozamiento:

quedando para el balance de energía:

Siendo a un factor de corrección de la velocidad, que para régimen laminar tiene el valor 0,5 y para régimen turbulento tiene el valor 1.

Si la ecuación de Bernuilli ([III.7]) se dividiese por g (m²/s), los términos quedarían expresados en unidades de longitud, denominados "cargas" y el término de pérdida de energía por rozamiento se denomina pérdida de carga, independientemente a sus unidades.

• Velocidad media.
• Propiedades del fluido
• Características de la conducción.

Régimen laminar: Balance macroscópico de cantidad de movimiento en un tubo cilíndrico (ecuación de Poiseuille):

de donde:

Régimen turbulento: Ecuación empírica, que puede obtenerse por análisis dimensional (ecuación de Fanning):

La presencia de codos, uniones, válvulas y otros accesorios o "accidentes" provoca pérdidas de carga adicionales; aunque individualmente son pequeñas, pueden tener una contribución total muy considerable.

Generalmente se determinan usando la ecuación de Fanning modificada: Se sustituye la longitud de la conducción, L, por una "longitud equivalente", L_e, longitud de conducción recta que produciría la misma pérdida de carga que el accidente correspondiente.

Los valores de la longitud equivalente de cada accidente están tabulados o representados en nomogramas (Figura III.6).

La energía de impulsión se calcula a partir de la ecuación de Bernuilli y luego se suele expresar como potencia suministrada:

No toda la potencia que acciona el equipo de impulsión se transforma en potencia útil, por lo que suele definirse el rendimiento:

• Cavitación: Evaporación que se produce cuando la presión en algún punto de la conducción desciende por debajo de la presión de vapor del líquido; si las burbujas alcanzan una zona de presión más elevada condensan violentamente pudiendo causar perforaciones en superficies sólidas. Se evitará si a la entrada de la bomba hay una presión superior al valor suministrado por el fabricante como carga neta positiva de aspiración, NPSH, (Net Positive Suction Head).
• Golpe de ariete: Onda de presión que se produce al detener bruscamente el flujo de un líquido y que puede ocasionar roturas en la conducción. Puede evitarse con un tanque hidroneumático, en el que la sobrepresión es absorbida mediante una cámara de aire.

En la impulsión de gases puede producirse compresión, que genera calor por efecto Joule; si se disipa el calor (isotérmico), el trabajo de compresión será mínimo, si se aisla la unidad de impulsión (adiabático), el trabajo de compresión será máximo. La situación real es intermedia y se llama "compresión politrópica".

Circulación de un fluido alrededor de objetos sumergidos; aplicaciones en Ingeniería Química:

• Operaciones de separación fluido - sólido (sedimentación, filtración).
• Operaciones básicas relacionadas con lechos de partículas.
• Circulación de fluidos entre bloques de tubos (cambiadores de calor).

Su estudio trata de obtener la relación entre la velocidad del fluido y la fuerza resistente que opone el sólido, principalmente debida a su forma.

• Diámetro de partícula, d_p: Diámetro de la esfera que posee el mismo volumen que la partícula:

de donde:

• Esfericidad, y: Relación entre la superficie de una esfera que posee el mismo volumen que la partícula y la superficie real de la partícula:

• Superficie específica, S_o: Superficie de la partícula por unidad de volumen de la partícula:

Generalizando a las condiciones definidas mediante:

Se obtiene la ecuación:

Donde f_D es el "coeficiente de arrastre" ("drag coefficient"), que habrá que determinar empíricamente.

que, para una esfera:

permite obtener el coeficiente de arrastre:

Conocido el coeficiente de arrastre y el área de la partícula, la fuerza de rozamiento puede calcularse de [III.19]:

Los lechos de partículas o "lechos porosos" tienen numerosas aplicaciones en Ingeniería Química:

• Operaciones de separación (filtración, adsorción), como inerte.
• Procesos químicos (intercambio iónico, catálisis heterogénea), como reactivo.

El paso del fluido a través de los huecos produce una "pérdida de carga", que hay que hacer mínima, sin perder eficacia.

Factores determinantes:

• Forma geométrica del sólido.
• Relación entre el tamaño de las partículas y la columna que las contiene.

Parámetro que caracteriza el lecho: porosidad o fracción de huecos:

Se aplican las ecuaciones de flujo interno, definiendo las condiciones del flujo mediante:

por lo que habrá que transformar los parámetros de las ecuaciones de flujo interno que se da en el interior de los canales (v y D), en los parámetros utilizados en el lecho poroso, v_o y d_p.

Considerando iguales relaciones entre superficies y volúmenes:

Aplicando la ecuación de continuidad:

Obteniéndose la ecuación:

Considerando los canales como cilindros, el volumen será:

es decir:

Considerando los canales como cilindros, la superficie será:

es decir:

Dividiendo ambas ecuaciones:

con lo cual:

Generalizando para otras geometrías:

se obtendría la ecuación de Carman-Kozeny (K = 150):

Para régimen turbulento (Re_l > 1.000), si se aplica la ecuación de Fanning al modelo:

se obtendría la ecuación de Burke-Plummer (K = 1,75):

Se pueden combinar linealmente ambas ecuaciones para cualquier régimen de circulación para obtener la ecuación de Ergun-Orning (K₁ = 150; K₂ = 1,75):

Cuando un fluido atraviesa un lecho poroso se produce una pérdida de carga que aumenta con la velocidad.

A velocidades altas del fluido las partículas del lecho comienzan a moverse, comportándose como un fluido; se habla de un "lecho fluidizado", de propiedades:

• Los objetos de menor densidad que el lecho fluidizado flotan en sus superficie.
• La superficie del lecho fluidizado permanece siempre horizontal, aunque se incline el recipiente.
• Si se practica un orificio en el recipiente que contiene el lecho fluidizado, éste se escapa por el orificio, como si fuese un líquido.
• Si dos lechos fluidizados se comunican entre sí, se produce la igualdad de niveles en los mismos (vasos comunicantes).

de donde:

Utilizando la ecuación de Carman-Kozeny para la pérdida de carga en régimen laminar:

puede obtenerse, igualando ambas ecuaciones:

de donde:

Los parámetros para esta ecuación en régimen laminar son:

con lo que se obtiene:

Como la porosidad del lecho suele ser de alrededor de 0,56, se obtiene que la velocidad de arrastre es de unas 20 veces mayor que la velocidad mínima de fluidización, lo que asegura ampliamente la estabilidad del lecho.

Gran importancia práctica: Flujo de una fase líquida alimentada por la parte superior de una columna rellena de partículas y de una fase gaseosa alimentada por la parte inferior.

Comportamiento característico de la caída de presión a través del relleno, no abordable de forma teórica, mostrado en la Figura III.10.

Si se hace circular líquido en contracorriente, para cierto valor de la velocidad del gas (X, "punto de carga"), la caída de presión aumenta más rápidamente, ya que el relleno se va llenando de líquido.

Para caudales de gas superiores (Y, "punto de inundación"), la caída de presión aumenta de forma muy pronunciada y la columna se inunda.

Suele trabajarse a velocidades de gas comprendidas entre 50 y 75% de la velocidad de inundación, que hay que calcular.

El cálculo de la velocidad de inundación se efectúa mediante la ecuación de Sawistowski: