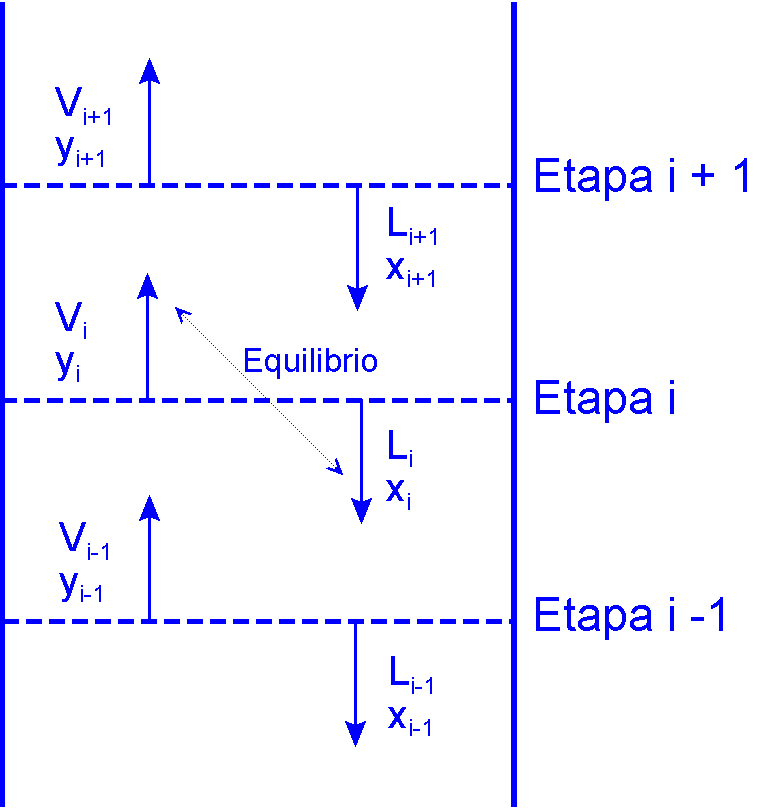
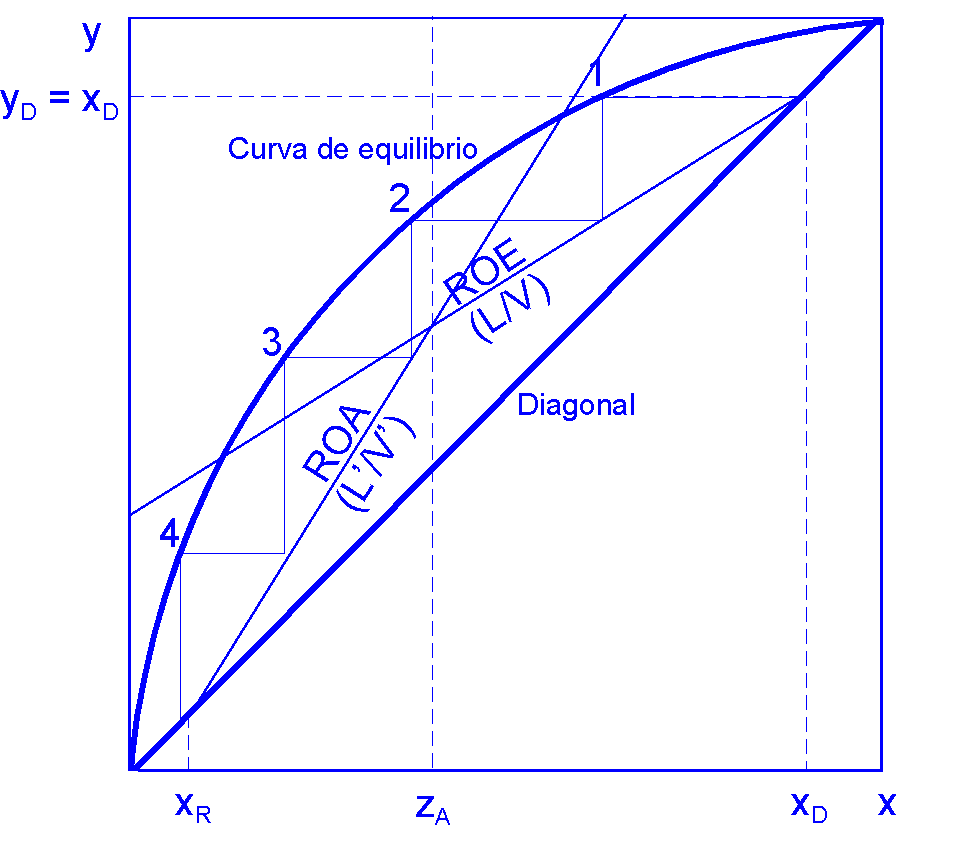
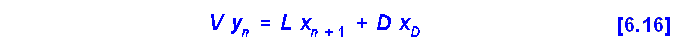| 6.2.1 Equilibrio líquido-vapor
Según la regla de las fases, a una presión y una temperatura fijadas, las composiciones de ambas fases están fijadas. Puede establecerse el equilibrio con las concentraciones relativas de un componente en cada una de las fases ("coeficiente de reparto"), combinando las leyes de Dalton y Raoult:
de donde
Las presiones de vapor de los componentes puros dependen de la temperatura, expresándose en forma tabular o analítica:
Muchas veces se usa el concepto de "volatilidad relativa", a:
que para sistemas binarios queda:
y permite obtener la relación y-x:
|
| IngQui (Tema 6) Operaciones de separación escogidas (4 de 37) |